Background Information

This example will look at the calculations for an axial loaded concrete column. We will solve for the nominal compressive strength and check moment utilization as well as the interaction capacity.

This example is based on the textbook Reinforced Concrete Structures: Analysis and Design. We will apply a load to determine the utilization of the given cross section. You can follow along on Access Engineering for more information and resources on concrete design, as well as the accompanying video.

Given Data

• Concrete compressive strength f’c = 12000 psi
• Reinforcement strength = 60 ksi
• Dead load = 120 000 lb
• Live load = 100 000 lb
• Loads are applied at an eccentricity of 10 in

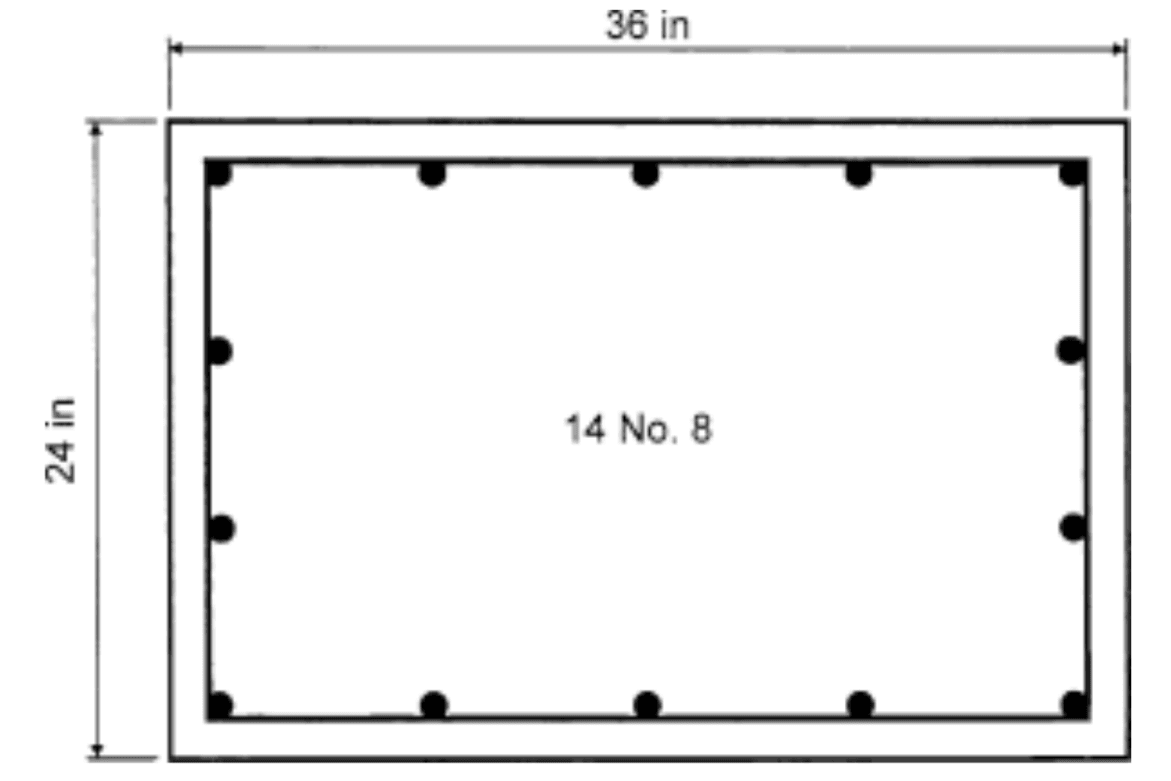
Reinforcement and cross sectional geometry can be found in the diagram below.

Inputting Key Properties

From the diagram in the example, we can take our cross sectional height as 24 in and cross sectional width as 36 in. The concrete strength was given as 12 ksi or 12 000 psi. Since we were not given a column length, we will assume this to be 12 ft. For this example, we will consider the column to be located in a non-sway frame. As a result, we can set the buckling length factor to be 1 so that it is conservative.

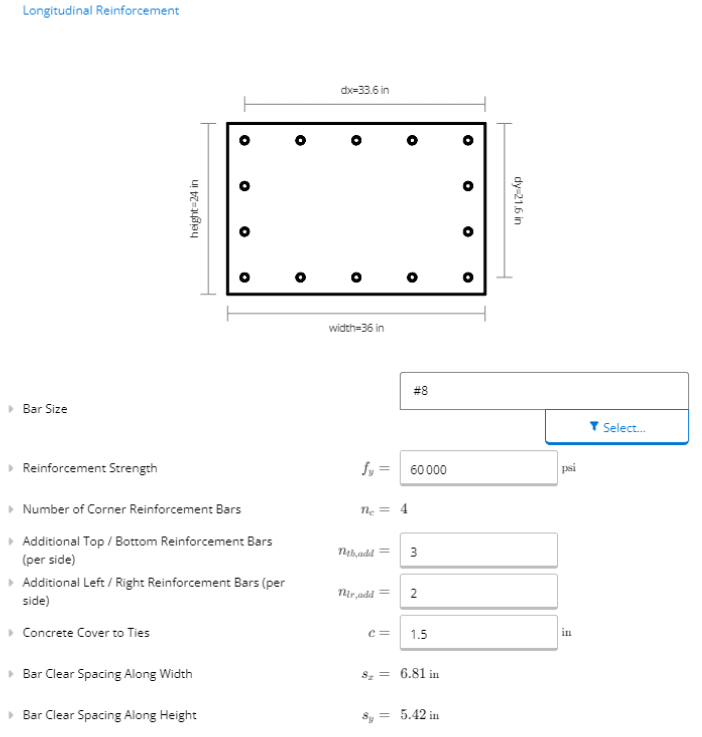
Longitudinal Reinforcement

The design example contained most of the reinforcement information. We can set our bar size to No. 8 bars, with a strength of 60 ksi. By default, ClearCalcs considers one bar at each corner of the column. To design the column such that we have 5 bars on the top and bottom, we can set the additional bars input to 3 (3 + 1 on each corner). Similarly, we can set additional bars on the left and right as 2, so we have 4 along each side. The concrete cover to ties can be set as 1.5 in, where this is the minimum value allowed by the code.

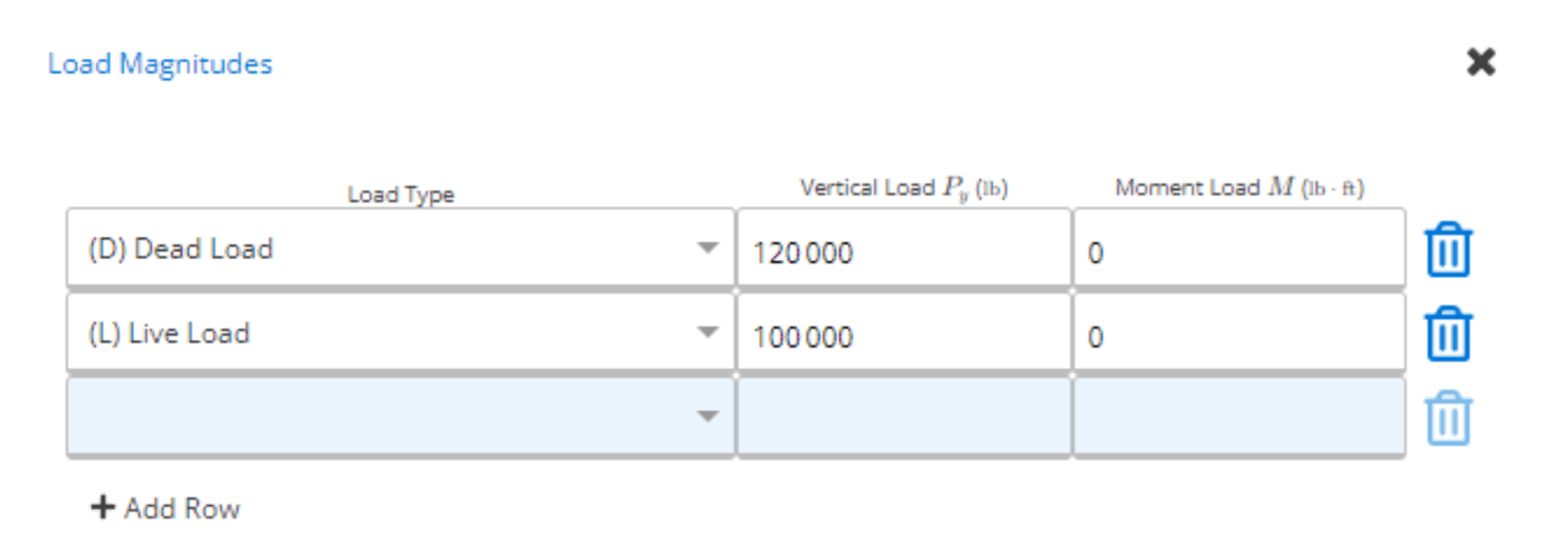
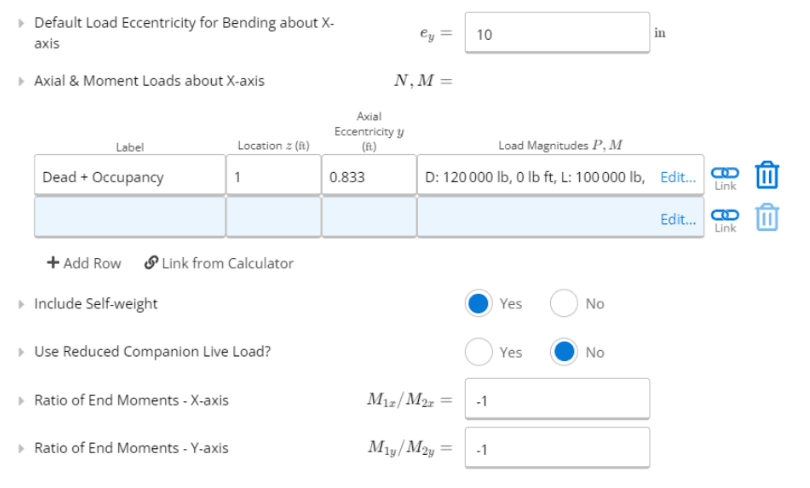
Load Inputs

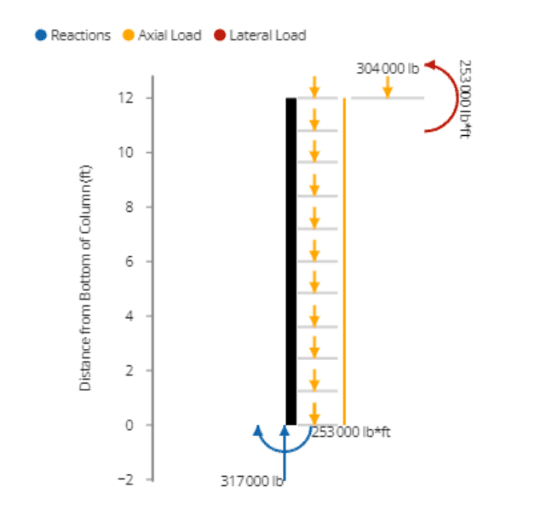
As given, we can set our loads to have a default 10 in eccentricity, this should be used if you have an applied load that is offset from the geometric centroid. We can input our dead loads and live loads in the “Axial & Moment Loads about X-axis” table. By clicking “Edit”, we can see the below dialogue and enter our live and dead loads. The vertical loads can be used to input axial loads which will cause compression or tension along the height of the column. On the other hand, an input in the moment loads will generate a rotation of the member about the x-axis. For our design, we can input the dead load as 120 kip, and the live load as 100 kip.

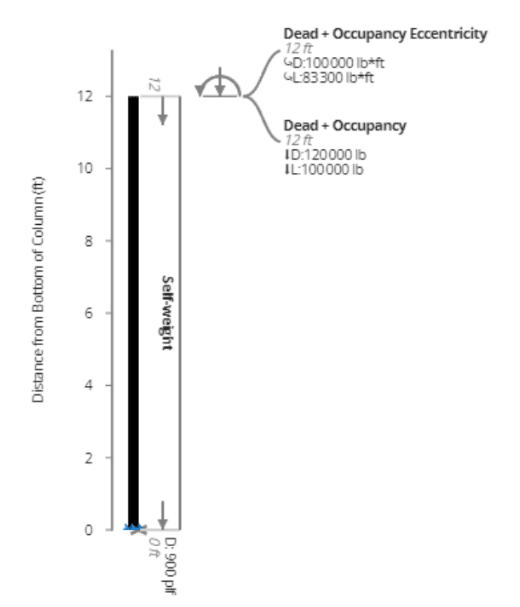
Since we only have live and dead loads, we do not need to consider the live load reduction allowed by IBC for load combinations with snow or rain. For the ratio of end moments, we assume that the column is in single-curvature bending, a generally conservative assumption. Therefore, we will have the moments at one end in opposing directions from the opposite end. Our ratio can be inputted here as -1. This value can also be determined from the tables in ACI 318-19.

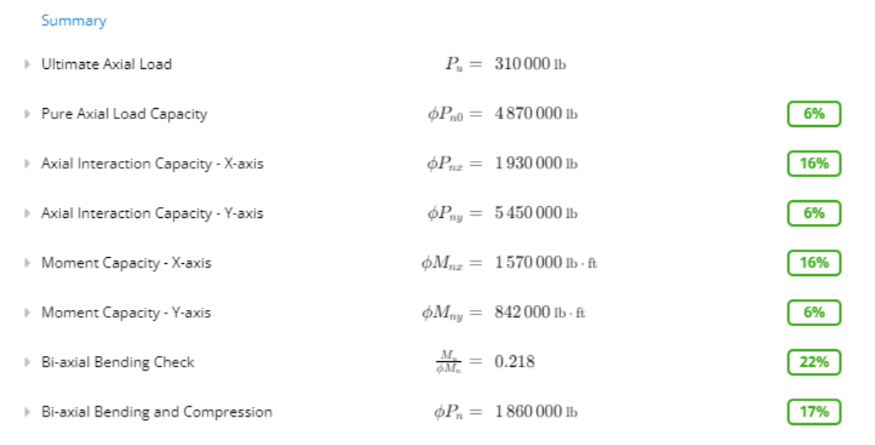
Summary of Results

Now that our design is complete, we can scroll back up to the top to see the summary of results. We can see that our design is governed by biaxial bending, with a 22% utilization. For a more efficient design, we could use a smaller cross section, say 20 in by 30 in. We could also adjust the bar size and diameter so we have less reinforcement, as long as the reinforcement ratio is still adequate.